Strongly-Typed Recurrent Neural Networks

This article does not present my own ideas. It is my analysis and thoughts on ideas published by others as I search for the guiding principles behind Deep Learning. In this article I present the need for a Deep Learning Principia, and then I explain the paradigm of Strongly-Typed Recurrent Neural Networks. You can skip the first half, but it builds the motivation to present the second half.

Basic knowledge of Recurrent Neural Networks is assumed.

A brief history on the Principia Mathematica

Before Sir Isaac Newton published “Philosophiæ Naturalis Principia Mathematica”, Science - or Natural Philosophy as they called it - was approached in two different ways. Majority of scientific research was either based on the principles of either deduction or induction. Definitions will help:

Deduction is an approach of drawing conclusions from the observation, based on the premises which are taken as the truth. The deduction is true, as long as the premise is true, i.e Deduction explains the observations on the basis of what we already know. This restricts the deductive methods to form conclusions when the premises haven’t been established.

Induction is an approach of testing new ideas and theories through repeated experimentation and making observations. However, the approach admits that the drawn conclusion can probably be wrong. This approach opens up the field of study to new ideas, admitting that the new ideas could be wrong too.

Newton - lost in the arguments from both sides - took a hybrid approach to study the natural phenomenon. He first established axioms by careful experimentation and observations, and then he built on the mathematical principles already established to formalize those axioms based on deduction. This step-wise generalization of observed data resulted in Principia Mathematica, which gave us the three laws of motions, laid down the principles of gravitation. He then mathematically explained Kepler’s elliptical orbits with his inverse square law.

A valid criticism of Principia was that Newton explained the laws of forces through his own mathematical models, but he could not explain the reason behind the forces. To which Newton replied that he had intended to explain the operations of gravity, and not what enabled gravity. There was an admittance of ignorance, but there was a new idea, a new way to look at the world. It provided the us with new mathematical tools and models to observe the world and is accepted by many as the greatest scientific work to have been published. It was these structured principles deriving from the methods of induction and deduction that advanced the scientific progress and eventually changed the world.

We lack these structured principles in Deep Learning but then it is a very new field. However, with the current rate of progress in the field with the amount of research being done, it is not too soon to search for a Deep Learning Principia.

The need for guiding principles in Deep Learning

The ideas that form the backbone of Deep Learning are properly structured. The working mechanism of the training process is well understood. The mathematics is clearly defined for the neuron, the loss function, the matrix operations and the architectures that we deploy. But we cannot explain why Deep Neural Networks(DNN) work so well. There are vague ideas floating about, but there is no solid research to support evidence. As we go deeper into the architectures, we start losing the sense of whatever abstractions each layer learns, hence the term ‘Black Box’ is prominent in media reports of Deep Learning research.

This however, has not stopped the innovation in the field. Carlos E. Perez draws an analogy between Deep Learning and Alchemy, in the sense that Deep Learning innovation is the result of concocting DNN architectures, mixing them with different hyperparameters and applying various cost functions. He has written a bold post questioning the need for “Is Deep Learning Innovation Just Due to Brute Force?”. It goes to show, that most of the research is deduction based, trying to explain the workings of a model based on theories that we already know.

I have come to realize that we do not understand the flow of information through these Deep Neural Networks. We do not understand what’s happening to the information as it passes through various Neural Network architectures. We have a vague idea that hidden layers learn a concise representation of the information, but we do not know how many such layers are appropriate to model the information to suit our needs, and we do not know what kind of layer is needed to model this information.

Many times I have read new research and wondered how the researchers designed a particular model. What thought process and what intuition, and most importantly, what mathematics? And the answer is almost always the same. They build upon their intuitions, and they try different architectures, choosing the ones that work the best. This naturally arises the doubt, can there be a better and a simpler model? Is it possible, that perhaps, we do not know enough about the information flow through these models, and thus we are limited by what we can design.

This shows the need for an inductive approach to bring out new ideas that define the mathematics of information flow, and one such paper that aims to do that is Strongly-Typed Recurrent Neural Networks.

Strongly-Typed Recurrent Neural Networks

This paper derives its ideas from physics and functional programming. In physics, we have the principle of homogeneity that constraints the operations between two quantities of different types. For example, you cannot add 27 Newtons of Force to 35 Kgs of mass.

Similarly, this paper explores the idea that perhaps information too is of different kinds, and changes its type as it flows through the Deep Neural Network. The authors have used beautiful phrasing:

"An exemplar is the system of measurement that has been carved out of nature by physicists. It prescribes units for expressing the readouts of standardized measuring devices (e.g. kelvin for thermometers and seconds for clocks) and rules for combining them."

Before I go into the technicalities of the paper, I want to reflect the sentiment expressed here. Physicists have observed the world and carved out a system of measurement for the naturally occurring phenomenon like heat, force, pressure etc., through inductive reasoning. And Demis Hassabis of Deep Mind believes that information is as fundamental being as energy or matter. So, It is only natural for researchers to carve out a new system of measurement for information, to develop a new kind of mathematics to understand the flow of information through Deep Neural Networks. And this paper is a beautiful step in that direction.

They introduce Strongly-Typed Quasi-Linear Algebra to represent the information flow in DNNs, and I explain the theorems in simple terms, as I understand them.

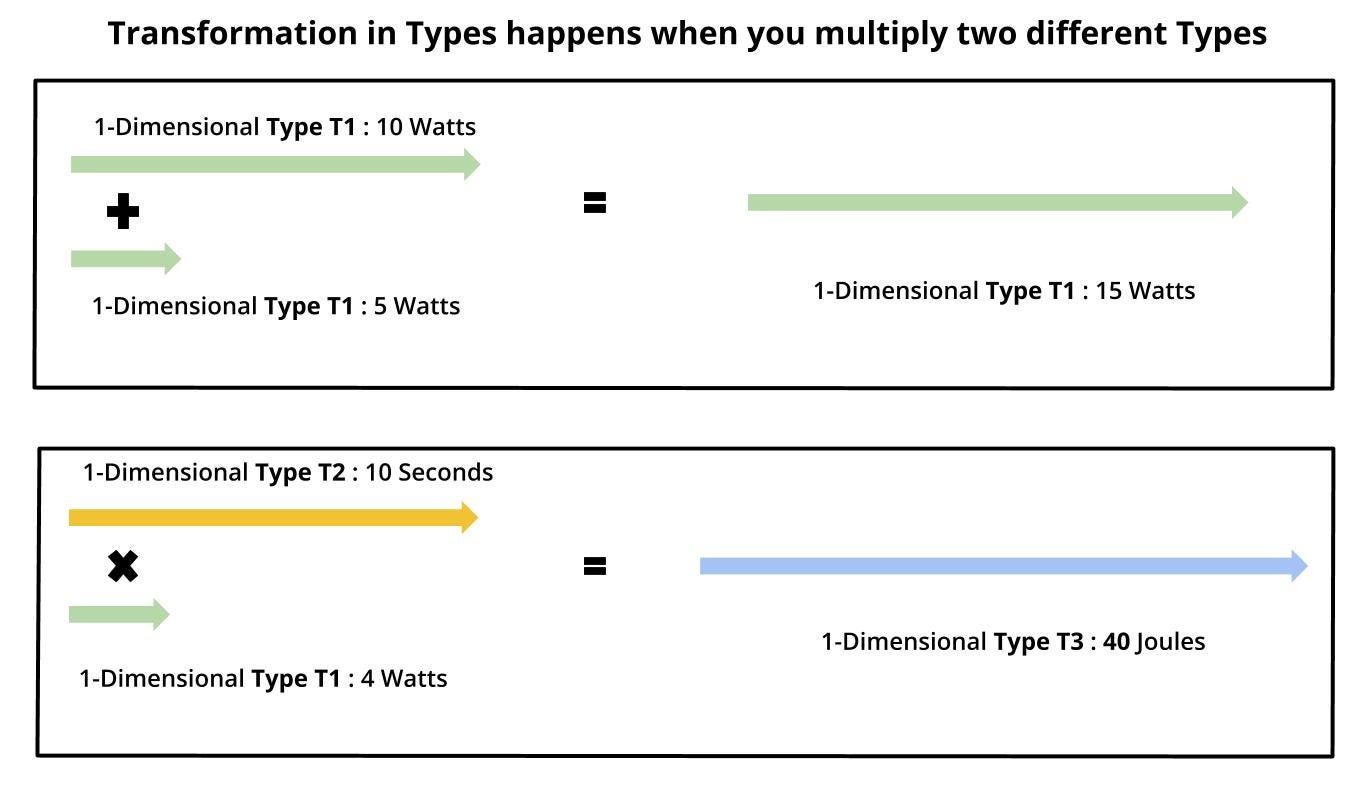
• Theorem 1: A Type(T) is a vector space with an orthogonal basis in ‘d’ dimensions. Just like a point in 2-dimensional Euclidean Space is represented by a combination of 2 orthogonal basis(the x coordinate, and the y coordinate; orthogonal means that the x and y coordinate are independent of each other), an information can be represented in a d-dimensional space called ‘Type’.

• Theorem 2: There can be many Types representing different interpretations of information. An information’s Type can change as it flows through different parts of the Deep Neural Networks.

• Theorem 3: An information can be changed by doing unary, or binary operations in that particular Type.

  • These operations preserve the Type of the information.
  • Binary operations between two different Types are not allowed.
  • This is similar to how the coordinates of a point in 2-D can be changed by doing unary, or binary operations on the x and y component in that particular 2-D Space.
    However, only a few operations are allowed.
    Unary operations: {tanh, relu, sigmoid, scalar multiplication etc.} Binary operations: {+, -, max, min}

I try to explain this paradigm of Types by drawing analogies with 1-D vector spaces:

• Theorem 4: A Type Transform (T1 → T2) is achieved by a matrix multiplication between two different types.

• Theorem 5: Elementwise multiplication between Type T1, and Type T2 results in a direct transformation of Type T1 into Type T2.
  This is different from Theorem 4, in the sense that ‘Matrix Multiplication’ of Type T1 with Type T2 will produce a Type T3. However, ‘Elementwise Multiplication’ of Type T1 with Type T2 will produce a Type T2.

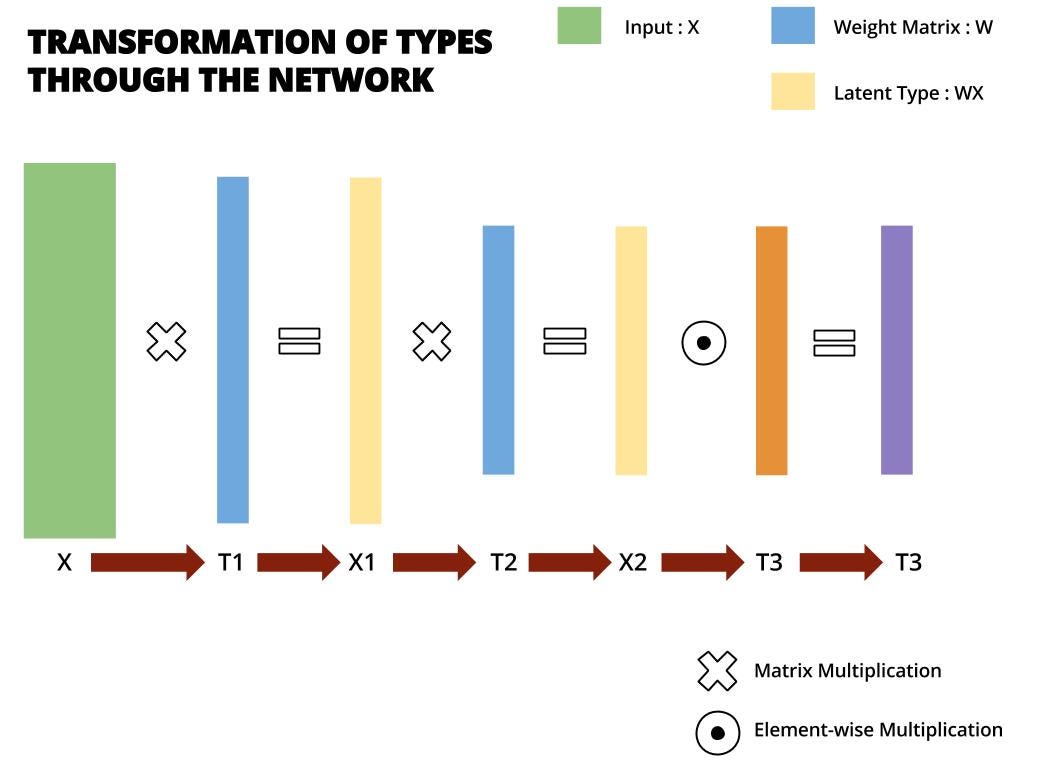
This is induction based reasoning. These operational patterns were laid down by observing the behaviour of RNNs. And where are they going with this?

These theorems classify Deep Neural Networks in two classes. Strongly-Typed(Type Consistent) and Weakly-Typed(Type Inconsistent).

If these constraints are applied to classical architectures - like vanilla RNNs, LSTMs, and GRUs - it seems that these classical networks are weakly-typed, i.e they have type inconsistencies arising from addition of two different types. Let’s take the example of LSTMs; the update equation is:

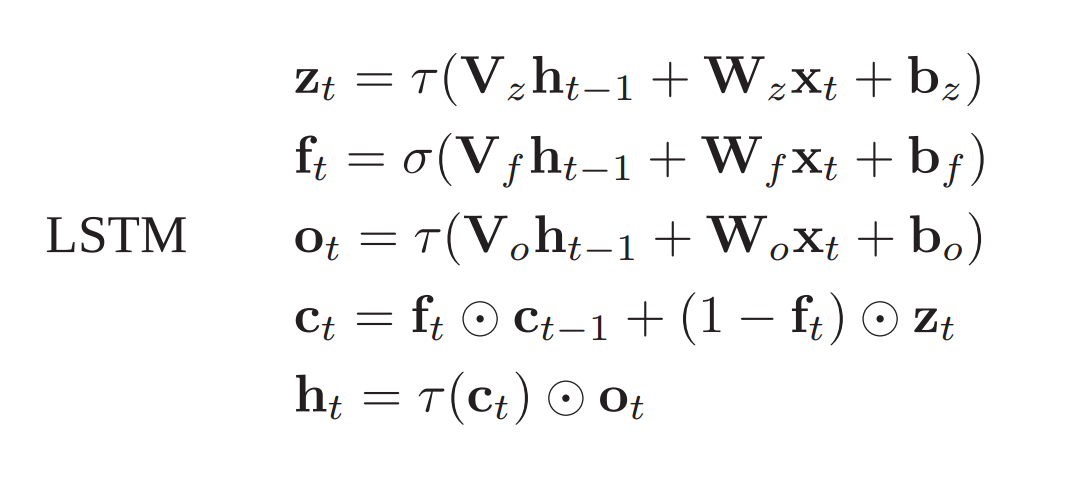
In the paper, a mathematical demonstration shows that this structure is type inconsistent, I have ommited the mathematical demonstration to keep the simplicity. However I provide an intuitive explanation. Consider the theorems stated above, output h[t] depends on it’s previous state h[t-1] and the input x[t]. So:

1. If we assume that h[t-1] is of Type H.
2. Assume that input x is of Type X.
3. Assume that weight matrices multiplied to h[t-1] and x[t], change their respective types to a single Type Y that enables binary operation between them. Meaning, that h[t] will be of Type Y.
4. Now, h[t] and h[t-1] represent same type of information across different timesteps. So, it must mean that Type Y is the same as Type H. i.e No Type Transformation takes place.
5. But, according to theorem 4 a matrix multiplication will result in a Type Transformation, essentially meaning that Type Y cannot be the same as Type H. This disproves the assumption we made in (4). So, Type Y is different from Type H. This is inconsistent because ‘h’ should maintain it’s Type across all states.

This happens because of the recurrence relation, where the current state depends on the previous state. In classical architectures,the recurrence relation also results in exploding gradients. So the authors introduce a new paradigm of designing RNN cells, inspired by functional programming. And this has resulted in much better and faster architectures, and it gives a perspective on the design of the cell whose equations have started looking beautiful to me.

The paradigm of Learnware and Firmware

We can’t remove the recurrence relation from RNNs, because recurrence defines RNNs. But, we can divide the RNN cell into two blocks. One block that does the learning, and other block that maintains the recurrence relation. The terminology is Learnware(state-less), and Firmware(state-dependant).

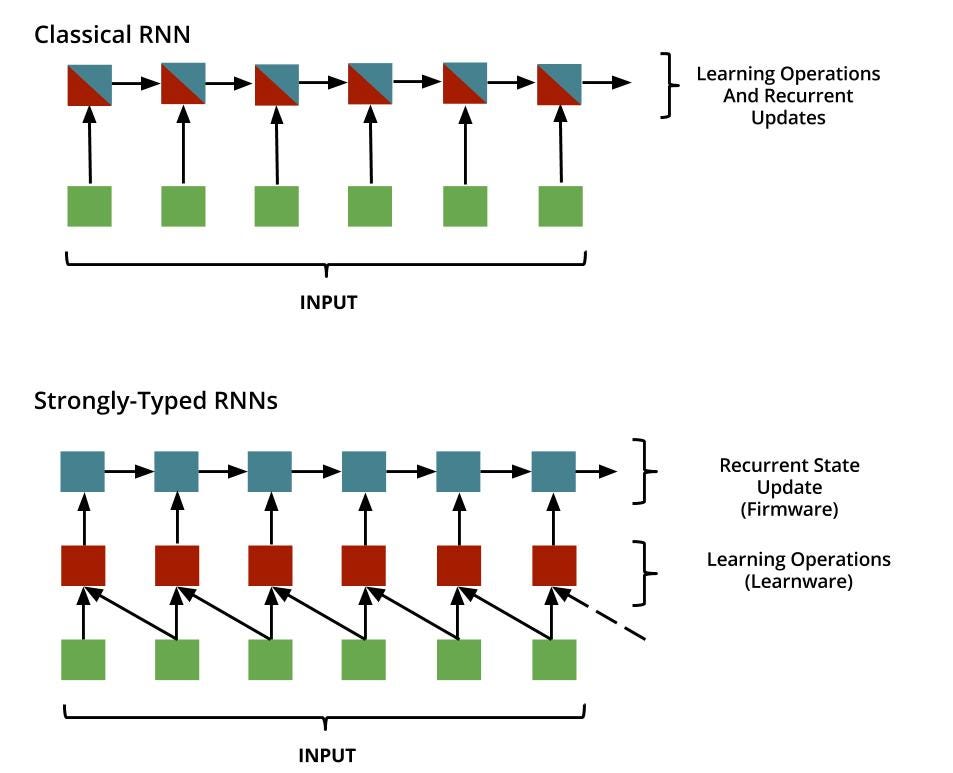
The idea is simple, yet powerful. Learnware will have learning parameters, dependent on only the inputs. And Firmware will take these learned parameters and do state-dependant recurrent operations to hold this memory. Notice that the distinction between the learning stage, and recurrent stage enables parallelism in the learning stage. This makes the computation much faster.

And since, no state update goes back into the learnware, there will not be any gradient explosions over long duration of time because learning is happening on the inputs. Which also means, that there is no need to apply non-linearity on the inputs to squash it. They prove this mathematically in the paper. And based on this paradigm, they design a new LSTM cell block, which is strongly-typed. They call this T-LSTMs:

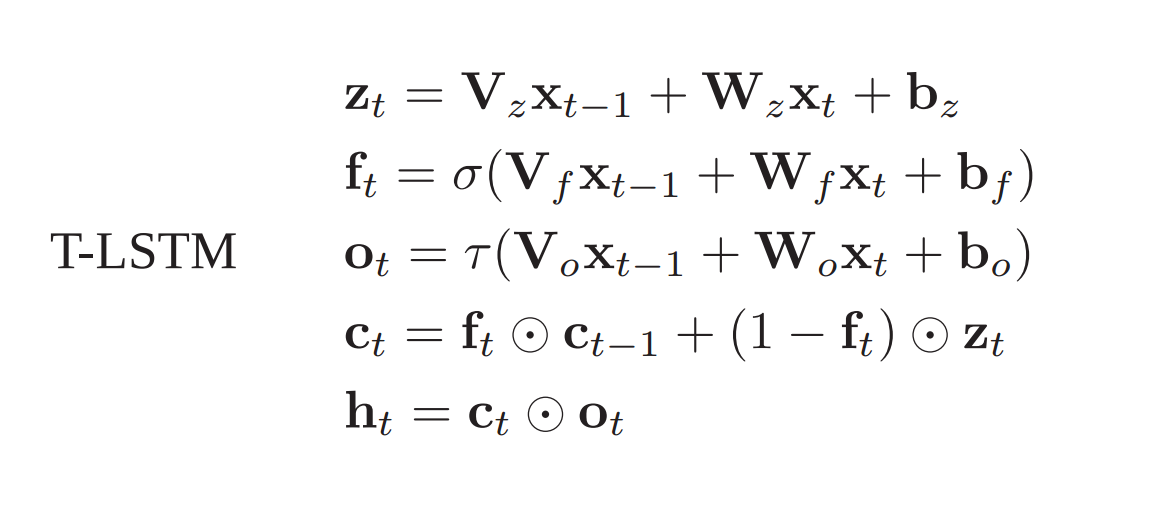
Take a look at these equations. The input gate, the forget fate and the output gate learn from the input data. And, the cell state holds the information that has to be passed to the next timestep, and output is dependant on this cell state and output gate. There are further explorations and inferences in the paper, but I will not go into the depths. When I get abundant computational resources, I will try those ideas out, myself. Anyhow, the advantages of Strong-Typed RNNs with my understanding are:

• Strong-Typing the information flow seems more reasonable than assuming all information is of the same kind.
• The distinction between Learnware and Firmware serves as a defining design principle, that is much easier to reason about than the classical design. It solves the problem of exploding gradients, and thus eliminates the need for gradient clipping.
• Strong-Typing with Learnware and Firmware distinction enables parallelism.
• Because of reduced nonlinearities, the computational complexities have decreased and the paper reports that Strong-Typed LSTMs are ~1.6 times faster than classical LSTMs.
• Element-wise state updates make the architecture more stable.
• Another interesting finding is that the strongly-typed architecture has lower training error in various tasks.

The strong-typed guiding principle showed marginally better results than the classical architectures, however, the authors have said that they did not experiment enough. Although later, QRNNs arrived, taking the learnings of Strong-Typed designs with an architecture that is 16 times faster than the classical LSTMs. So, I conclude that this idea of constraining the information flow has some weight, and needs to be explored further.

On an ending note, I will again emphasize the need for a Deep Learning Principia. I personally need it, to try different architectures, but I lack resources to experiment on the scale that research labs do. And my intuition says that Strongly-Typed Deep Learning will not lead to Artificial Intelligence but to draw further on the analogy between Deep Learning and Alchemy; Alchemy was practiced to achieve an ambitious goal to find the elixir of life - just like Deep Learning is trying to solve Intelligence - but instead, we found Chemistry. And boy, did that turn out well.

I thank David Balduzzi, for helping me understand the ideas behind this paper.

Citation